Tips 若看不到公式,刷新一下即可。
现象
前些天师弟们以开环驱动陀螺的方式做实验,利用信号发生器直接产生一定频率的余弦波信号去激励陀螺,以步长为1Hz调整信号频率。
理论上来讲,如果陀螺处于谐振状态,激励信号的相位应该超前陀螺输出信号90度。然而,利用示波器观察激励信号和陀螺输出信号的相位,发现在某个频率点附近,小1Hz的频率会使激励信号和陀螺输出信号同相位;而大1Hz的频率会使激励信号和陀螺输出信号反相位。
控制层面
师弟是学自动化出身的,于是尝试从控制层面去解释该现象。谐振式陀螺可以看做一个二阶系统,其相频特性决定在谐振点附近会从~0度快速下降到~-180度。
为了更清晰地说明这个过程,我们尝试利用伯德图进行分析。假设陀螺传递函数为:
\[G(s)=\frac{1}{s^2+s+628}\]利用MATLAB分别画出两个陀螺的伯德图:
clear;
close all;
num = [1];
den = [1,0.1,628];
sys=tf(num,den) %输出传递函数
bode(sys)
grid on;
h= findobj(gcf,'type','line');
set(h(3),'linewidth',1.5); %调整幅值曲线线宽
set(h(4),'linewidth',1.5); %调整相位曲线线宽
title('High Q factor');
程序运行结果为:
sys =
1
---------------
s^2 + s + 628
Continuous-time transfer function.
绘制图片为:
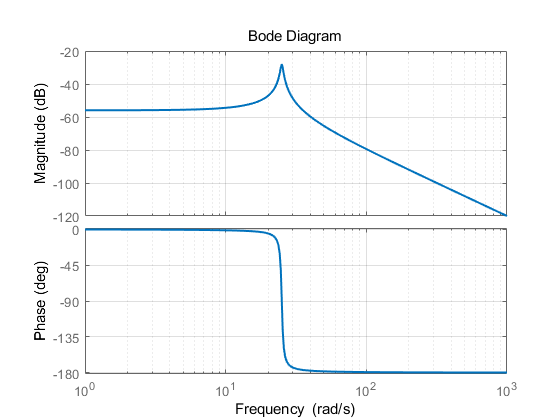
观察伯德图可以看出,在共振点(谐振点)附近的相位变化较为剧烈,可以实现细微的频率变化导致同相或反相。如此即可解释激励信号和陀螺输出信号同相或反相的问题。
以上都是基于经典控制理论的感性分析,我们尝试利用机械振动的理论进一步深入探究。
振动层面
为了简化问题,直接分析无阻尼受迫振动。设如下动力学方程:
\[\ddot{x}+\omega_{0}^{2} x=F \cos \omega t\]设该二阶微分方程的解为:
\[x=A \sin \omega t+B \cos \omega t\]将其代入原式可得:
利用待定系数法,比较等式两边系数得到:
\[%\begin{cases} A=0 \\ B=\frac{F}{\omega_{0}^{2}-\omega^{2}} %\end{cases}\]于是得到微分方程的解为:
\[x(t)=\frac{F}{\omega_{0}^{2}-\omega^{2}} \cos \omega t\]观察上式可以看出,若 $\omega_0>\omega$,微分方程的解(即陀螺输出信号)前面的系数为正,振动(陀螺输出信号)与驱动(激励信号)同相;若 $\omega_0<\omega$,微分方程的解前面的系数为负,振动与驱动反相。
阻尼
由于实验用的陀螺具有超高Q值(极低阻尼),考虑相位的剧烈变化与阻尼有关,采用上述MATLAB代码进一步对低Q值(高阻尼)和极低Q值(超高阻尼)的二阶系统绘制伯德图。
低Q值系统:
\[G(s)=\frac{1}{s^2+5s+628}\]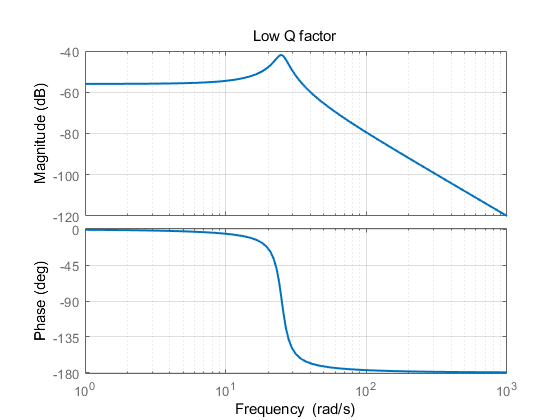
增大阻尼(降低Q值)后,相频特性曲线明显不如高Q值的陡峭,也即相频特性收到阻尼的影响。
极低Q值系统:
\[G(s)=\frac{1}{s^2+50s+628}\]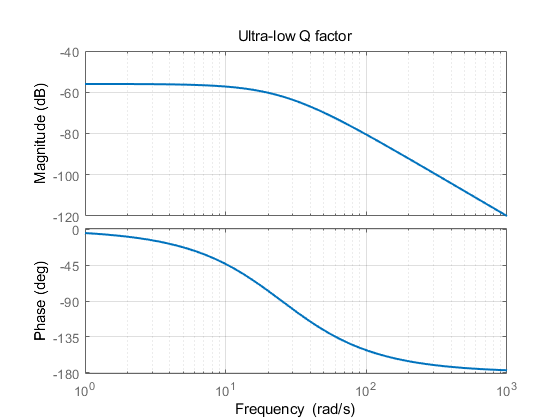
进一步增加阻尼,相频曲线再次变缓,幅频曲线近似一阶系统。分析原因是由于一阶项对应系数远大于二阶项对应系数,因此主要表现出一阶特性。由此可见,保证较小的阻尼对于谐振式陀螺具有一定的实际意义。